سیگما چیست؟
رکنا: در ریاضیات، سیگما (∑) نماد جمع است که برای نمایش جمع مقادیر یا عبارتها بهکار میرود. این نماد معمولاً بهصورت ∑ از i = a تا b (∑_(i=a)^b) استفاده میشود تا مجموع مقادیر یک دنباله را از i = a تا i = b نشان دهد.
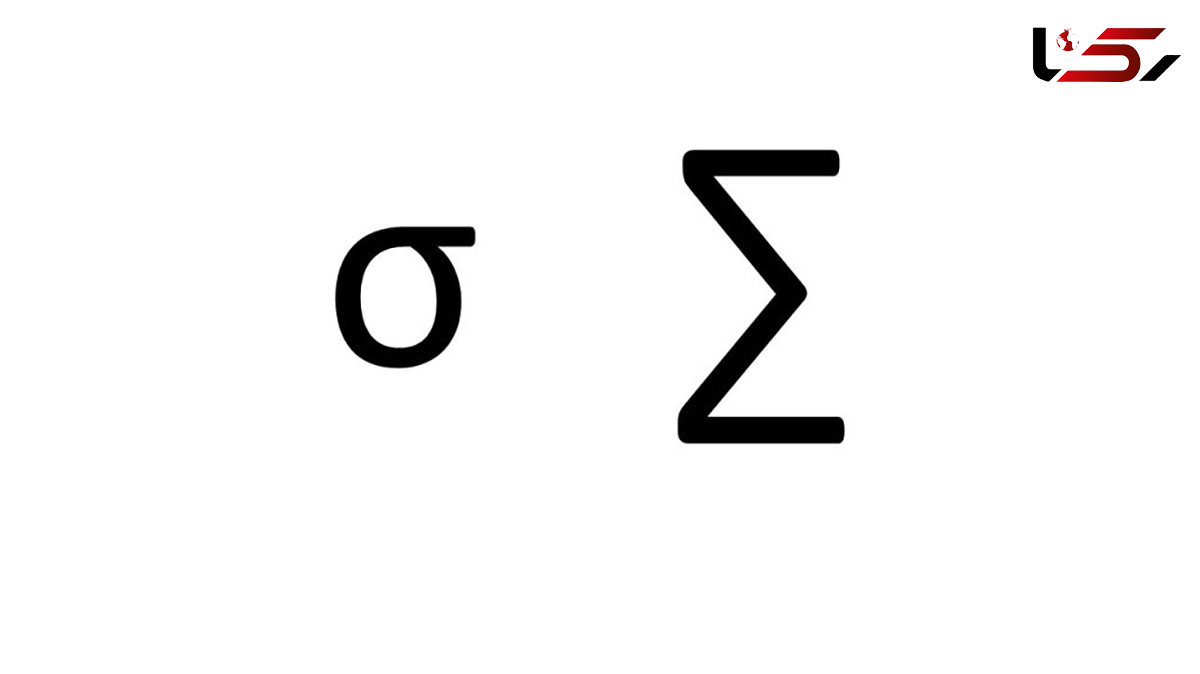
به گزارش خبرنگار رکنا، سیگما (σ) یک حرف یونانی است که در ریاضیات و همچنین علوم مختلف به کار میرود.
سیگما؛ نمادی با قدمتی طولانی در ریاضیات
سیگما (Σ)، حرف شانزدهم الفبای یونانی، در ریاضیات نمادی بسیار مهم و پرکاربرد است که برای نمایش جمعهای سریالی به کار میرود. اما تاریخچه استفاده از این نماد در ریاضیات به چه زمانی برمیگردد؟
ریشه های تاریخی سیگما در ریاضیات
یونان باستان: یونانیان باستان از اولین مردمانی بودند که به ریاضیات علاقه نشان دادند. آنها از نمادهای مختلفی برای نمایش مفاهیم ریاضی استفاده میکردند و سیگما نیز یکی از این نمادها بود.
قرون وسطی: در طول قرون وسطی، با گسترش دانش ریاضی، استفاده از نماد سیگما نیز رواج یافت. ریاضیدانان مسلمان و اروپایی از این نماد برای نمایش مجموعهای پیچیدهتر استفاده میکردند.
دوران رنسانس: در دوران رنسانس، با ظهور علم جدید و پیشرفت ریاضیات، استفاده از نمادهای ریاضی به طور گستردهای رایج شد. سیگما نیز به عنوان یک نماد استاندارد برای نمایش مجموعها پذیرفته شد.
دوران مدرن: در دوران مدرن، با توسعه شاخههای مختلف ریاضی مانند آنالیز، آمار و احتمال، استفاده از سیگما به شدت افزایش یافت. امروزه، سیگما یکی از اساسیترین نمادهای ریاضی است که در همه سطوح آموزشی و تحقیقاتی مورد استفاده قرار میگیرد.
چرا سیگما؟
انتخاب حرف سیگما (Σ) به عنوان نماد برای نمایش مجموع، دلایل مختلفی دارد:
صدا: صدای حرف سیگما در زبان یونانی به معنای "جمع" یا "با هم" است که با مفهوم ریاضی آن همخوانی دارد.
شکل: شکل حرف سیگما شبیه به حرف S در الفبای لاتین است که به معنای "sum" (جمع) در زبان انگلیسی است.
سادگی و کارایی: سیگما یک نماد ساده و در عین حال قدرتمند است که به راحتی قابل درک و استفاده است.
کاربردهای مدرن سیگما
امروزه، سیگما در بسیاری از زمینهها از جمله:
ریاضیات پایه: نمایش مجموع دنبالهها، محاسبه مجموع جملات یک سری
آمار و احتمال: محاسبه میانگین، واریانس، همبستگی و سایر شاخصهای آماری
فیزیک: محاسبه کار، انرژی، و سایر کمیتهای فیزیکی
اقتصاد: محاسبه درآمد کل، هزینه کل و سایر شاخصهای اقتصادی
علوم کامپیوتر: الگوریتمهای جستجو و مرتبسازی
و بسیاری از زمینههای دیگر کاربرد دارد.
در نتیجه، سیگما یک نماد ریاضی با قدمتی طولانی است که از زمان یونان باستان تاکنون مورد استفاده قرار میگیرد. سادگی، کارایی و ارتباط معنایی آن با مفهوم جمع، باعث شده است که این نماد به یکی از اساسیترین نمادهای ریاضی تبدیل شود.
حوزه های استفاده از سیگما
سیگما (σ) به طور گسترده در حوزههای مختلف علمی و حتی در روانشناسی به کار میرود. در اینجا توضیحاتی بیشتر در مورد هر یک از کاربردهای آن:
| حوزه | کاربرد سیگما | مثال |
|---|---|---|
| ریاضیات پایه | نمایش مجموع یک دنباله | ∑ᵢ₌₁ⁿ aᵢ = a₁ + a₂ + ... + aₙ |
| محاسبه مجموع جملات یک سری | ∑ᵢ₌₁∞ (1/2)ⁱ | |
| آمار و احتمال | محاسبه میانگین | x̄ = (1/n) ∑ᵢ₌₁ⁿ xᵢ |
| محاسبه واریانس | σ² = (1/n) ∑ᵢ₌₁ⁿ (xᵢ - x̄)² | |
| محاسبه امید ریاضی | E(X) = ∑xᵢ p(xᵢ) | |
| محاسبات عددی | تقریبزنی انتگرالها | ∫a^b f(x) dx ≈ ∑ᵢ₌₁ⁿ f(xᵢ) Δx |
| فیزیک | محاسبه کار انجام شده توسط یک نیرو | W = ∑Fᵢ Δxᵢ |
| محاسبه انرژی کل یک سیستم | E = ∑Eᵢ | |
| اقتصاد | محاسبه درآمد کل | TR = ∑PᵢQᵢ |
| محاسبه هزینه کل | TC = ∑Cᵢ | |
| علوم کامپیوتر | الگوریتمهای جستجو و مرتبسازی | (در بسیاری از الگوریتمها از سیگما برای محاسبه زمان اجرای الگوریتم استفاده میشود) |
| روانشناسی | تحلیل دادههای کمی | محاسبه میانگین نمرات آزمون، واریانس ویژگیهای شخصیتی، و ... |
| مدلسازی | استفاده در مدلهای آماری برای پیشبینی رفتارها و پدیدههای روانشناختی | |
| متاآنالیز | ترکیب نتایج چندین مطالعه برای رسیدن به نتیجهگیری قویتر |
1. سیگما در ریاضیات:
علامت مجموع (Σ): در ریاضیات، سیگما به عنوان نماد مجموع (Summation) شناخته میشود. این علامت برای نشان دادن جمع مقادیر مختلف استفاده میشود. به عبارت دیگر، سیگما معادلهای است که نشان میدهد یک سری از اعداد باید با یکدیگر جمع شوند.
سیگما به شما این امکان را میدهد که جمع مجموعهای از مقادیر را به طور فشرده نمایش دهید، به جای نوشتن تمامی اعضای آن.
تابع سیگما (σ): در نظریه اعداد، تابع سیگما به مجموع مقسومعلیههای یک عدد طبیعی اشاره دارد.
2. سیگما در آمار:
انحراف معیار (σ): سیگما یکی از مهمترین شاخصهای آماری است که میزان پراکندگی دادهها نسبت به میانگین را اندازهگیری میکند. به طور خاص، انحراف معیار نشان میدهد که دادهها تا چه اندازه از میانگین دور هستند.
به عبارت دیگر، اگر انحراف معیار (σ) کوچک باشد، دادهها نزدیک به میانگین قرار دارند، و اگر بزرگ باشد، دادهها پراکندهتر هستند.
3. سیگما در فیزیک:
ثابتهای فیزیکی: در فیزیک، سیگما ممکن است به عنوان نمادهایی برای مقادیر مختلف استفاده شود. به عنوان مثال:
در رابطه فشار-حجم در ترمودینامیک، سیگما به عنوان یک نماد برای ویژگیهای مختلف سیستم گاز یا مایعات به کار میرود.
در نظریه میدانهای الکترومغناطیسی، سیگما میتواند به عنوان یک نماد برای شارش یا جریان میدان استفاده شود.
سیگما در فرهنگ عامه و روانشناسی
در سالهای اخیر، اصطلاح "سیگما" به دنیای مجازی راه یافته و معنای جدیدی به خود گرفته است. سیگما در این زمینه معمولاً برای توصیف افرادی استفاده میشود که:
مستقل و خودکفا هستند: آنها به دنبال تأیید دیگران نیستند و بر اساس ارزشها و باورهای شخصی خود عمل میکنند.
اعتماد به نفس بالایی دارند: سیگماها به تواناییهای خود اطمینان دارند و از شکست نمیترسند.
غیرقابل پیشبینی هستند: آنها از قالبهای از پیش تعیین شده پیروی نمیکنند و راههای جدیدی را برای زندگی انتخاب میکنند.
به دنبال موفقیتهای شخصی هستند: سیگماها به دنبال دستیابی به اهداف خود هستند و برای رسیدن به آنها تلاش میکنند.
تفاوت سیگما با آلفا
ممکن است سیگما را با آلفا مقایسه کنید. در حالی که آلفاها معمولاً به عنوان رهبران و افراد با نفوذ شناخته میشوند، سیگماها ترجیح میدهند خارج از سلسله مراتب قرار بگیرند. سیگماها به دنبال قدرت بر دیگران نیستند، بلکه به دنبال آزادی و استقلال شخصی هستند.
ویژگی های یک فرد سیگما
| ویژگی | توضیح |
|---|---|
| استقلال | ترجیح میدهند به جای دنبال کردن گروه، مسیر خود را طی کنند. |
| خودکفا | به دیگران وابسته نیستند و به تنهایی به اهداف خود میرسند. |
| اعتماد به نفس بالا | به تواناییهای خود اطمینان دارند و از شکست نمیترسند. |
| درونگرا | انرژی خود را از درون میگیرند و معمولاً به جمعهای بزرگ علاقهای ندارند. |
| خلاق | به دنبال راه حلهای نوآورانه برای مشکلات هستند. |
| هدفمند | اهداف مشخصی دارند و برای رسیدن به آنها برنامهریزی میکنند. |
| غیرقابل پیشبینی | از قالبهای از پیش تعیین شده پیروی نمیکنند. |
| مسئولیتپذیر | مسئولیت اعمال و تصمیمات خود را میپذیرند. |
| انگیزه درونی | انگیزه آنها برای موفقیت از درون برمیخیزد. |
| مقاومت در برابر فشار گروه | تحت تأثیر نظرات دیگران قرار نمیگیرند. |
درونگرا: سیگماها معمولاً درونگرا هستند و انرژی خود را از درون میگیرند.
خلاق: آنها به دنبال راه حلهای جدید و نوآورانه برای مشکلات هستند.
مستقل: سیگماها به تنهایی کار کردن را ترجیح میدهند و به دیگران وابسته نیستند.
هدفمند: آنها اهداف مشخصی دارند و برای رسیدن به آنها برنامهریزی میکنند.
نکته مهم: مفهوم سیگما در حال تکامل است و تعاریف مختلفی از آن وجود دارد. این مفهوم لزوماً با تیپهای شخصیتی شناخته شده مانند MBTI همخوانی ندارد.
آیا می توان افراد را به طور قطعی به عنوان سیگما، آلفا یا بتا طبقه بندی کرد؟
خیر، نمیتوان افراد را به طور قطعی و مطلق به عنوان سیگما، آلفا یا بتا طبقهبندی کرد. این تقسیمبندیها بیشتر مدلهای سادهسازیشدهای از واقعیت هستند که برای درک بهتر رفتارهای انسانی و تعاملات اجتماعی استفاده میشوند.
چرا این تقسیم بندی ها ساده سازی شده هستند؟
پیچیدگی شخصیت انسان: شخصیت انسان بسیار پیچیده و چند وجهی است و نمیتوان آن را به چند دسته ساده تقسیم کرد. هر فرد مجموعهای منحصر به فرد از ویژگیها، تجربیات و باورها است که در تعامل با محیط پیرامونش شکل میگیرد.
تغییرات شخصیتی: شخصیت انسان در طول زمان تغییر میکند و تحت تأثیر عوامل مختلفی مانند سن، تجربیات، روابط و رشد شخصی قرار میگیرد.
بستگی به موقعیت: رفتار افراد در موقعیتهای مختلف متفاوت است. فردی که در یک موقعیت خاص به عنوان سیگما رفتار میکند، ممکن است در موقعیت دیگری به عنوان آلفا عمل کند.
عدم وجود مرزهای دقیق: بین این تیپهای شخصیتی مرزهای دقیقی وجود ندارد و افراد میتوانند ترکیبی از ویژگیهای مختلف را داشته باشند.
چرا با وجود این محدودیت ها، از این تقسیم بندی ها استفاده می شود؟
سادگی و درک بهتر: این مدلها به ما کمک میکنند تا رفتارهای انسانی را بهتر درک کنیم و الگوهای کلی را شناسایی کنیم.
ارتباطات اجتماعی: این مدلها میتوانند به ما در برقراری ارتباط بهتر با دیگران کمک کنند. با شناخت ویژگیهای کلی هر تیپ شخصیتی، میتوانیم پیشبینی بهتری از رفتار افراد داشته باشیم و روابطمان را بهبود بخشیم.
خودشناسی: این مدلها میتوانند به افراد کمک کنند تا خودشان را بهتر بشناسند و نقاط قوت و ضعف خود را شناسایی کنند.
در نهایت، مهم است به خاطر داشته باشیم که این تقسیمبندیها ابزارهایی برای درک بهتر انسان هستند و نباید به عنوان واقعیت مطلق به آنها نگاه کرد. هر فردی منحصر به فرد است و نمیتوان او را به طور کامل در یک قالب خاص قرار داد.
-
بابک حمیدیان، ستاره درخشان سریال «تاسیان»: مردم وقتی منو میبینن هیجان زده نمیشن، میگن عه اینه چون ....











ارسال نظر