قطر چیست؟ / جداول هندسی قطر + سوالات قابل توجه
رکنا: قطر یکی از اندازه های مهم در بسیاری از اشکال هندسی است که می توان از آن برای محاسبه اندازه های دیگر مانند طول ضلع، محیط، مساحت و غیره استفاده کرد.
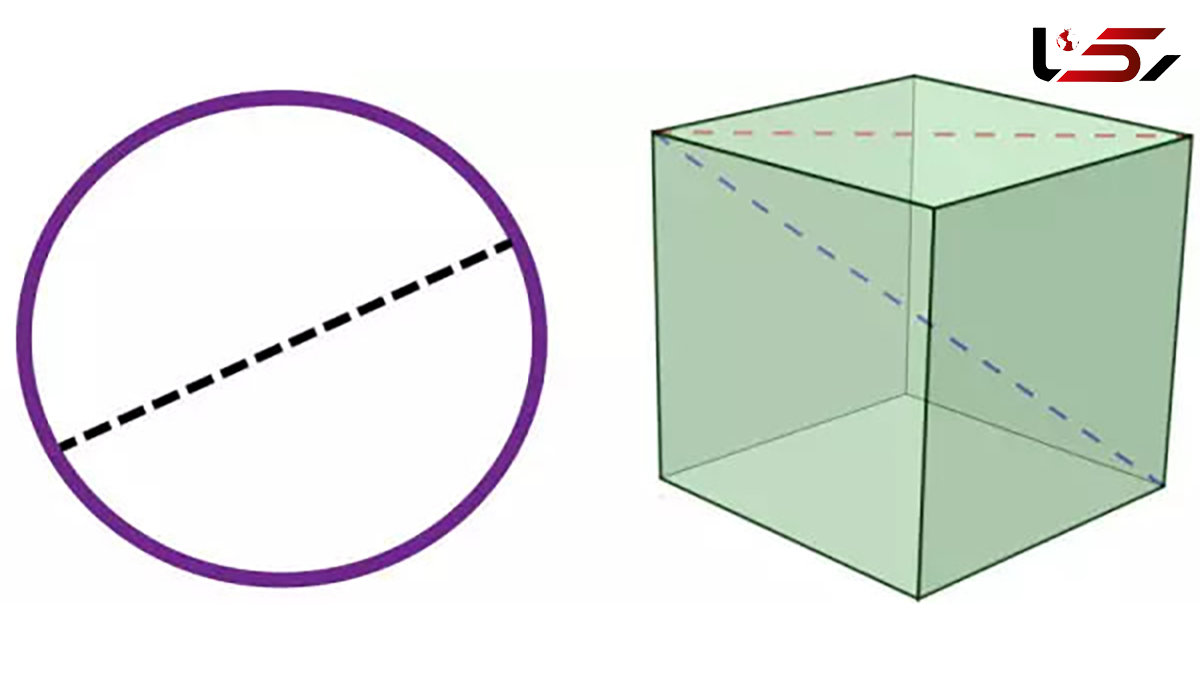
به گزارش رکنا، در هندسه قطر به خطی گفته میشود که دو نقطه از یک چندضلعی یا دایره را به هم متصل میکند، به طوری که از مرکز شکل عبور نکند. به عبارت دیگر:
در یک دایره، قطر خطی است که از مرکز دایره عبور میکند و دو نقطه روی دایره را به هم متصل میسازد. طول قطر دایره برابر با دو برابر شعاع دایره است.
در چندضلعیهای منتظم (مانند مربع یا مستطیل)، قطر به خطی اطلاق میشود که دو رأس از اضلاع غیرمجاور را به هم وصل میکند.
برای مثال:
در دایرهای با شعاع rr، طول قطر برابر با 2r2r است.
در یک مربع، دو قطر به هم عمود هستند و هر کدام از رأسها را به رأس مخالف خود متصل میکنند.
قطر (Diagonal) به پارهخطی گفته میشود که دو راس غیرمجاور در چندضلعیها یا چندوجهیها را به هم متصل میکند. در دایره، قطر به پارهخطی اطلاق میشود که از مرکز عبور کرده و دو نقطه از محیط دایره را به یکدیگر وصل میکند.
قطر در هندسه، بسته به شکل هندسی که با آن سروکار داریم، معانی مختلفی دارد:
در چندضلعیها:
قطر یا تراکُنج: پاره خطی است که دو رأس غیر مجاور یک چندضلعی را به هم متصل میکند. به عبارت سادهتر، خطی است که از یک گوشه شکل به گوشه روبروی آن کشیده شود و از هیچ ضلعی عبور نکند.
در دایره:
قطر یا ترامون: پاره خطی است که از مرکز دایره گذشته و دو سر آن روی محیط دایره قرار میگیرد. به عبارت دیگر، بلندترین وتر دایره است. همه قطرهای یک دایره با هم برابرند.
ویژگیهای قطر
قطر در دایره، دایره را به دو نیمه مساوی تقسیم میکند.
طول قطر در دایره دو برابر شعاع آن است.
تعداد قطرهای یک چندضلعی با افزایش تعداد اضلاع افزایش مییابد.
کاربردهای قطر
محاسبه مساحت و محیط برخی اشکال هندسی
تقسیم اشکال به بخشهای مساوی
اثبات قضایای هندسی
مثالها:
قطر مربع، خطی است که دو گوشه مقابل مربع را به هم وصل میکند.
قطر مستطیل، خطی است که دو گوشه مقابل مستطیل را به هم وصل میکند.
قطر دایره، خطی است که از مرکز دایره گذشته و دو نقطه روی محیط دایره را به هم وصل میکند.
قطر در چندضلعیها
«چندضلعی» (Polygon) به شکل هندسیای گفته میشود که از یک خط شکسته بسته تشکیل شده و شامل چندین ضلع، راس و زاویه است. در یک چندضلعی، قطر به پارهخطی گفته میشود که دو راس غیرمجاور را به هم متصل میکند. برای رسم قطر یک چندضلعی، باید از یکی از راسها شروع کرده و پارهخطی را به یکی از راسهای غیرمجاور وصل کنیم.
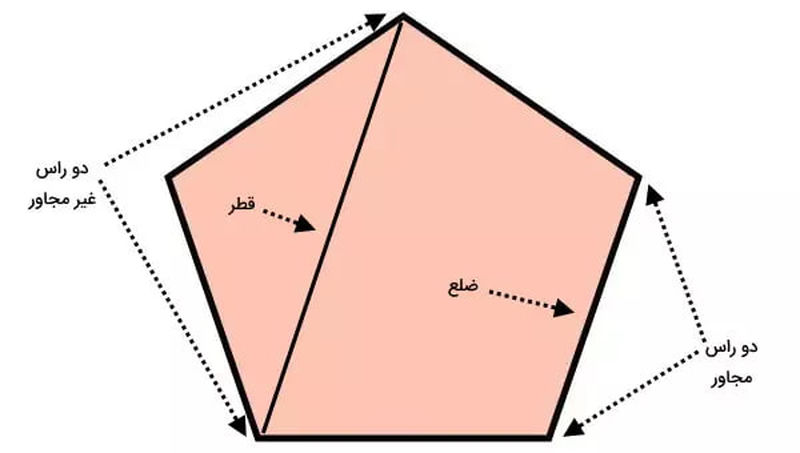
تفاوت ضلع و قطر در چندضلعیها
ضلع (یا لبه) چندضلعی، پارهخطی است که دو راس مجاور را به هم وصل میکند، در حالی که قطر پارهخطی است که دو راس غیرمجاور را به هم میپیوندد. این تفاوت اصلی بین ضلع و قطر در چندضلعیها است.
سوالات جالب درباره قطر در هندسه
در اینجا چند سوال جالب درباره قطر در هندسه آورده شده است که میتواند ذهن شما را درگیر کرده و به درک بهتر این مفهوم کمک کند:
چند قطر در یک مربع وجود دارد؟
سوالی ساده اما جالب! آیا میدانید که یک مربع دارای دو قطر است که طول آنها برابر با یکدیگر است و یکدیگر را در وسط مربع قطع میکنند؟
آیا در یک مثلث قطر وجود دارد؟
مثلث یک شکل هندسی با سه ضلع است. آیا میتوان برای مثلث قطری تعریف کرد؟ چرا یا چرا نه؟
چه رابطهای بین طول قطر یک دایره و شعاع آن وجود دارد؟
اگر شعاع دایره rr باشد، طول قطر دایره چقدر خواهد بود؟ (این سوال را میتوان با استفاده از فرمول D=2rD=2r پاسخ داد)
چند قطر در یک دایره وجود دارد؟
آیا قطرهای مختلف در یک دایره میتوانند از هم متفاوت باشند یا همه آنها برابرند؟ (جواب این سوال این است که همه قطرها در یک دایره برابرند!)
آیا میتوان برای یک پنجضلعی مقعر قطر رسم کرد؟
در یک پنجضلعی مقعر، آیا میتوان قطر رسم کرد؟ اگر بله، چطور؟ (در این نوع چندضلعیها، ممکن است قطرها از داخل یا خارج چندضلعی عبور کنند.)
اگر دو قطر در یک مستطیل با هم تداخل کنند، چه چیزی به وجود میآید؟
وقتی دو قطر در یک مستطیل با هم قطع میشوند، آیا آنها همیشه یکدیگر را در وسط مستطیل قطع میکنند؟ چرا؟
آیا در یک دایره فقط یک قطر وجود دارد؟
این سوال به بررسی تعداد قطرهای ممکن در یک دایره میپردازد. چرا تنها یک قطر وجود ندارد؟ (جواب این است که در یک دایره، تعداد بینهایتی قطر وجود دارد که همگی از مرکز عبور میکنند.)
آیا در یک هشتضلعی، قطرها همیشه همطول هستند؟
برای یک هشتضلعی منتظم، آیا همه قطرها برابر هستند؟ چه ویژگیهایی باعث میشود این اتفاق بیفتد؟
این سوالات به بررسی دقیقتر مفهوم قطر در اشکال هندسی مختلف کمک کرده و باعث میشوند که به جنبههای مختلف این مفهوم توجه کنید.
پاسخ به سوالات درباره قطر هندسی
در اینجا پاسخهایی برای سوالات مختلف درباره قطر در هندسه آورده شده است:
1. چند قطر در یک مربع وجود دارد؟
در یک مربع دو قطر وجود دارد. این دو قطر برابر هستند و در وسط مربع یکدیگر را قطع میکنند.
2. آیا در یک مثلث قطر وجود دارد؟
در یک مثلث هیچ قطری وجود ندارد. زیرا برای تعریف قطر، نیاز به داشتن حداقل چهار راس است و مثلث فقط سه راس دارد.
3. چه رابطهای بین طول قطر یک دایره و شعاع آن وجود دارد؟
طول قطر یک دایره برابر با دو برابر شعاع دایره است. فرمول آن به شکل زیر است:
D=2r
D=2r که در آن DD قطر و rr شعاع دایره است.
4. چند قطر در یک دایره وجود دارد؟
در یک دایره تعداد بینهایتی قطر وجود دارد. همه قطرهای دایره از مرکز عبور میکنند و طول یکسانی دارند.
5. آیا میتوان برای یک پنجضلعی مقعر قطر رسم کرد؟
در یک پنجضلعی مقعر نیز مانند سایر چندضلعیها، قطرهایی وجود دارند که دو راس غیرمجاور را به هم متصل میکنند. در این حالت، ممکن است بعضی از قطرها از داخل و برخی از آنها از خارج چندضلعی عبور کنند.
6. اگر دو قطر در یک مستطیل با هم تداخل کنند، چه چیزی به وجود میآید؟
در یک مستطیل، دو قطر همیشه در وسط مستطیل یکدیگر را قطع میکنند. این تقاطع در مرکز مستطیل است و زاویه بین این دو قطر 90 درجه است.
7. آیا در یک دایره فقط یک قطر وجود دارد؟
خیر. در یک دایره تعداد بینهایتی قطر وجود دارد. هر خطی که از مرکز دایره عبور کند و دو نقطه از محیط دایره را به هم وصل کند، یک قطر خواهد بود.
8. آیا در یک هشتضلعی، قطرها همیشه همطول هستند؟
در یک هشتضلعی منتظم، همه قطرها همطول هستند. این بدان معناست که هر قطر از مرکز هشتضلعی عبور کرده و طول یکسانی دارند.
9. در یک مربع قطرها چگونه با یکدیگر ارتباط دارند؟
در یک مربع، دو قطر برابر با یکدیگر هستند و همدیگر را در وسط مربع قطع میکنند. این دو قطر عمود بر یکدیگر هستند.
10. چه تفاوتی بین ضلع و قطر در یک چندضلعی وجود دارد؟
ضلع پارهخطی است که دو راس مجاور یک چندضلعی را به هم متصل میکند. در حالی که قطر پارهخطی است که دو راس غیرمجاور یک چندضلعی را به هم وصل میکند.
این پاسخها به شما کمک میکنند تا درک بهتری از مفهوم قطر در هندسه پیدا کنید و بتوانید آن را در اشکال هندسی مختلف بررسی کنید.
جداول اختصاصی قطر در هندسه
در هندسه، برای اشکال مختلف هندسی، تعداد و ویژگیهای قطرها قابل محاسبه هستند. در زیر جداولی برای تعداد قطرها و ویژگیهای آنها در برخی از اشکال هندسی مختلف آورده شده است.
جدول 1: تعداد قطرها در چندضلعیها
| تعداد اضلاع (n) | تعداد قطرها |
|---|---|
| 3 (مثلث) | 0 |
| 4 (مربع یا مستطیل) | 2 |
| 5 (پنجضلعی) | 5 |
| 6 (ششضلعی) | 9 |
| 7 (هفتضلعی) | 14 |
| 8 (هشتضلعی) | 20 |
| 9 (نهضلعی) | 27 |
| 10 (دهضلعی) | 35 |
توضیحات:
- برای یک چندضلعی با nnn ضلع، تعداد قطرها برابر با n(n−3)2\frac{n(n-3)}{2}2n(n−3) است.
- در مثلث هیچ قطری وجود ندارد زیرا همه راسها به یکدیگر متصل هستند.
جدول 2: ویژگیهای قطر در اشکال هندسی مختلف
| شکل هندسی | تعداد قطرها | ویژگیهای قطرها |
|---|---|---|
| دایره | بینهایت | همه قطرها از مرکز عبور میکنند و طول یکسان دارند. |
| مربع | 2 | قطرها عمود بر هم و برابر با یکدیگر هستند. |
| مستطیل | 2 | قطرها برابر با یکدیگر و در وسط مستطیل قطع میشوند. |
| پنجضلعی منتظم | 5 | قطرها همطول و از مرکز چندضلعی عبور میکنند. |
| ششضلعی منتظم | 9 | قطرها از مرکز عبور میکنند و همطول هستند. |
| هشتضلعی منتظم | 20 | قطرها از مرکز عبور کرده و به شکلهای مختلفی تقسیم میشوند. |
| دوازدهضلعی منتظم | 54 | قطرها از مرکز عبور کرده و بهطور منظم توزیع میشوند. |
جدول 3: قطر در چندوجهیها
| نوع چندوجهی | تعداد قطرها | ویژگیها |
|---|---|---|
| مکعب | 4 | قطرهای مکعب از گوشهها به گوشههای مخالف متصل میشوند. |
| هرم مربعی | 4 | در هرم مربعی، قطرهای مربع پایه وجود دارند که طول یکسان دارند. |
| هرم مثلثی | 0 | هیچ قطر مستقیمی در هرم مثلثی وجود ندارد. |
| منشور مثلثی | 6 | در منشور مثلثی، قطرها از راسهای مختلف در دو پایه به هم متصل میشوند. |
توضیحات:
در چندوجهیها، قطر به خطی گفته میشود که دو راس غیرمجاور را به هم متصل میکند. تعداد قطرها بستگی به تعداد راسها و نوع چندوجهی دارد.
این جداول به شما کمک میکنند تا درک بهتری از تعداد و ویژگیهای قطرها در اشکال هندسی مختلف پیدا کنید.













ارسال نظر